Distribution Of X According To The Central Limit Theorem
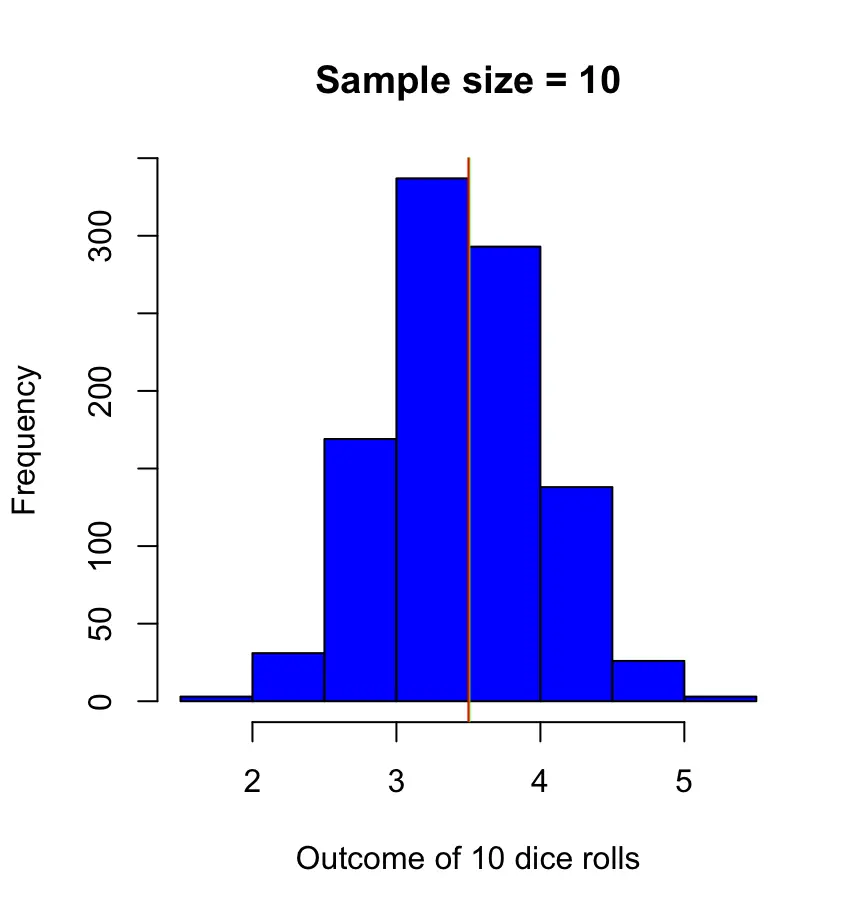
Distribution Of X According To The Central Limit Theorem. Law of Large Numbers: The larger the size of the sample, the more likely the mean of the sample will be close to the mean of the population. Introduction to the central limit theorem and the sampling distribution of the meanWatch the next lesson.
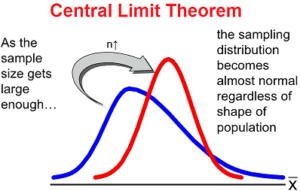
According to the Central Limit Theorem under certain conditions, the arithmetic mean of a sufficiently large number of iterates of independent random variables, each with a well-defined expected value and well-defined variance, will be approximately normally distributed, regardless of the distribution of.
Before jumping into the answer I would like to quote the central limit theorem, which according to me is the most fundamental theorem in statistics.
Week 5 ppt.
The Normal Distribution and what it can be used for - ECstep
Central Limit Theorem - Definition, Formula and Applications
Central Limit Theorem
Quick Graphs On Normal Distribution, Skewness, Mean ,Mode ...
Solved: (1 Point) Suppose A Random Variable X Is Normally ...
Solved: 7.According To The Central Limit Theorem, For Any ...
Clarifying a Step in Central Limit Theorem Derivation ...
The Sampling Distribution of the Sample Mean
Then, according to the central limit theorem, as n becomes large in the limit, the PDF of. The normal distri-bution has a mean equal to the original mean multiplied by the sample size and a standard. i want to observe central limit theorem and wrote this program. In probability theory, the central limit theorem (CLT) states that, in many situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution.
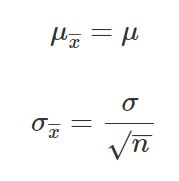
0 Response to "Distribution Of X According To The Central Limit Theorem"
Posting Komentar