The Value Of K According To Binomial Theorem
The Value Of K According To Binomial Theorem. Binomial Theorem forms part of the broader heading of Algebra in JEE Main Mathematics section. According to the theorem, the polynomial (x + y)n can be expanded into a sum involving terms of the form axbyc, where the exponents b and c are.
According to this theorem, it is possible to expand the polynomial "(a + b)n" into a sum involving terms of the form "axzyc", the exponents z and c are non-negative integers where z + c = n.
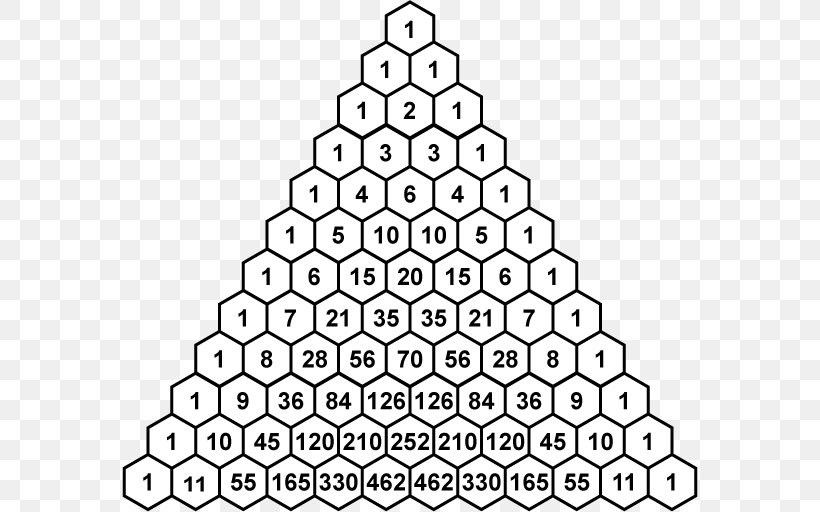
So it states that the coefficients of all the monomials in the expression a + b to the power of n are actually the numbers from the nth's row of Pascal's triangle, so.
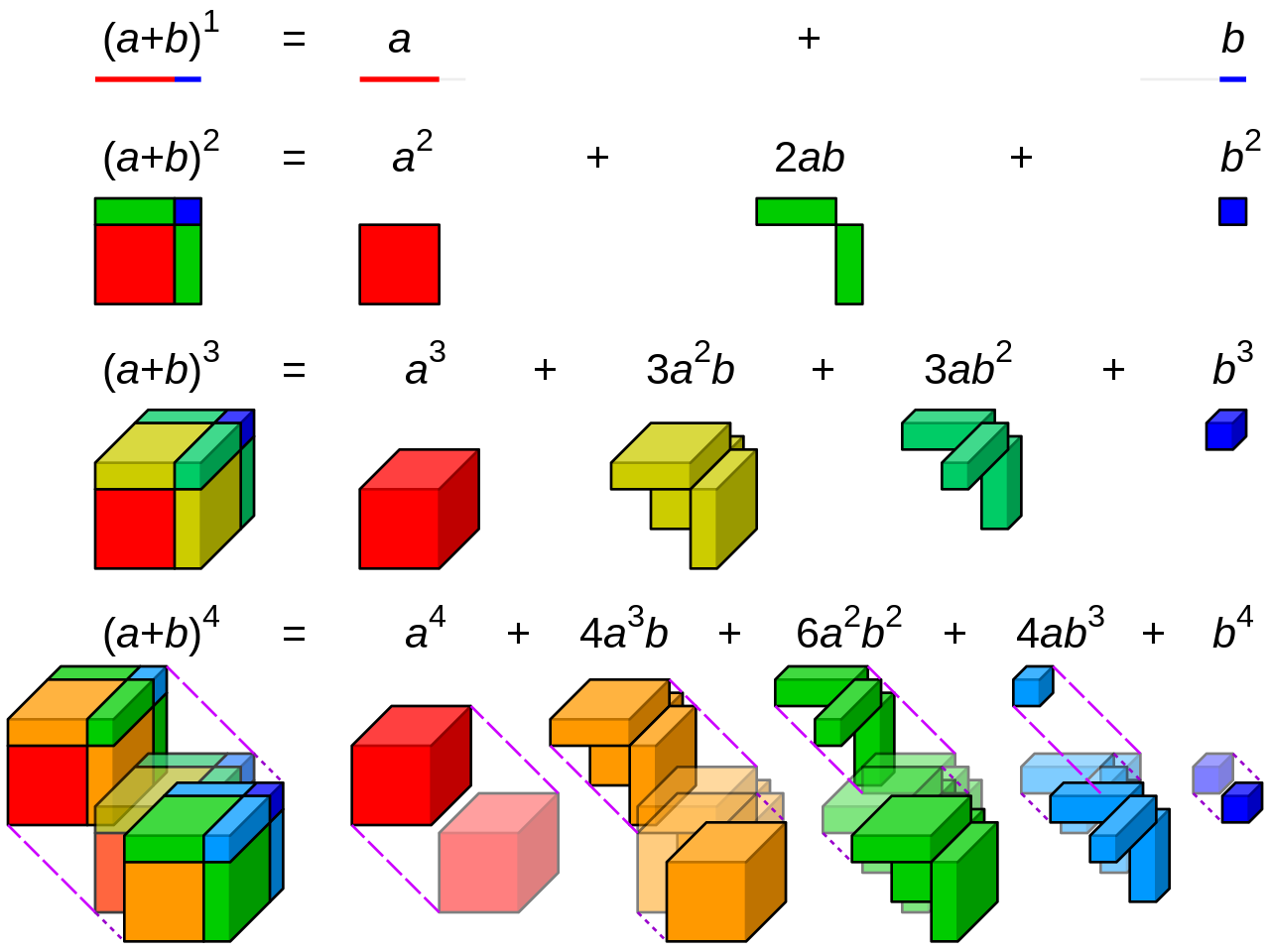
The middle term of the binomial coefficient varies according to the value of n. We have already learned to multiply binomials and to raise binomials to powers, but raising a Given a binomial, write a specific term without fully expanding. Binomial theorem or expansion describes the algebraic expansion of powers of a binomial.


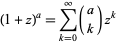

.jpg?mode=max&width=1025)
0 Response to "The Value Of K According To Binomial Theorem"
Posting Komentar